Video: Kako pronalazite ograničenja racionalnog izražavanja?
2024 Autor: Miles Stephen | [email protected]. Zadnja promjena: 2023-12-15 23:36
The ograničenje je da nazivnik ne može biti jednak nuli. Dakle, u ovom problemu, budući da je 4x u nazivniku, ne može biti jednako nuli. Pronađite sve vrijednosti x koje vam daju nulu u nazivniku. Da biste pronašli ograničenja na a racionalno funkciju, pronađite vrijednosti varijable koje čine nazivnik jednakim 0.
Na taj način, može li racionalni izraz imati bez ograničenja?
Pa isto je istina za racionalni izrazi . Drugi racionalno izražavanje je nikad nula u nazivniku i tako nemamo potreba Brinuti o bilo kakvih ograničenja . Također imajte na umu da brojnik drugog racionalno izražavanje volje biti nula. Da je dobro, mi samo potreba kako bi se izbjeglo dijeljenje s nulom.
Osim gore navedenog, kako rješavate racionalne izraze? Koraci za rješavanje racionalne jednadžbe su:
- Pronađite zajednički nazivnik.
- Pomnožite sve sa zajedničkim nazivnikom.
- Pojednostaviti.
- Provjerite odgovor(e) kako biste bili sigurni da nema stranog rješenja.
Drugo, zašto navodimo ograničenja za racionalno izražavanje i kada navodimo ograničenja?
Odgovor Provjeren stručnjak Racionalni izrazi su oni koji imaju razlomke. Navodimo ograničenja jer može uzrokovati da jednadžba bude nedefinirana u nekim vrijednostima x. Najčešći ograničenje za racionalne izraze je N/0. To znači da je svaki broj podijeljen s nulom nedefiniran.
Kako rješavate racionalne algebarske izraze?
- Riješenje:
- Korak 1: Faktorite sve nazivnike i odredite LCD.
- Korak 2: Identificirajte ograničenja. U ovom slučaju, oni su x≠−2 x ≠ − 2 i x≠−3 x ≠ − 3.
- Korak 3: Pomnožite obje strane jednadžbe s LCD-om.
- Korak 4: Riješite rezultirajuću jednadžbu.
- Korak 5: Provjerite ima li stranih rješenja.
Preporučeni:
Zašto navodimo ograničenja za racionalno izražavanje i kada navodimo ograničenja?
Navodimo ograničenja jer to može uzrokovati da jednadžba bude nedefinirana u nekim vrijednostima x. Najčešće ograničenje za racionalne izraze je N/0. To znači da je svaki broj podijeljen s nulom nedefiniran. Na primjer, za funkciju f(x) = 6/x², kada zamijenite x=0, rezultat bi bio 6/0 što je nedefinirano
Kako mogu primijeniti dimenzijska ograničenja u AutoCAD-u?
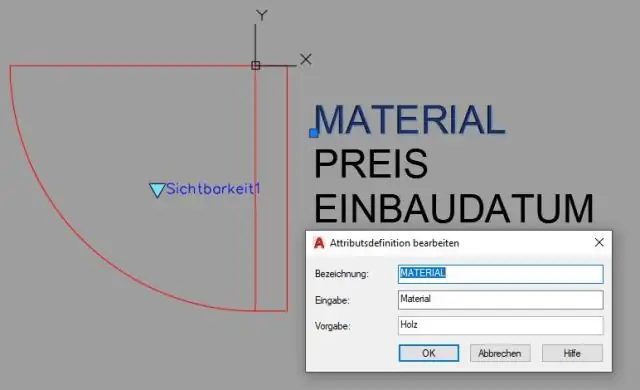
Ovi koraci predstavljaju jednostavan primjer dimenzionalnih ograničenja: Pokrenite novi crtež i učinite karticu Parametric vrpce trenutnom. Uključite odgovarajuća pomagala za precizno crtanje na statusnoj traci, kao što su Snap, Ortho i Osnap. Nacrtajte neku razumno preciznu geometriju primjenom precizne tehnike
Što je značenje racionalnog korijena?
Test racionalnih korijena. Test racionalnih korijena (također poznat kao Teorem o racionalnim nulama) omogućuje nam da pronađemo sve moguće racionalne korijene polinoma. Drugim riječima, ako zamijenimo a u polinom P (x) Pleft(x ight) P(x) i dobijemo nulu, 0, to znači da je ulazna vrijednost korijen funkcije
Koja izjava najbolje opisuje isključene vrijednosti racionalnog izraza?
Isključena vrijednost racionalnog izraza su vrijednosti kod kojih je nazivnik izraza nula. Također, broj nula polinoma uvijek je manji ili jednak stupnju polinoma. Dakle, broj isključenih vrijednosti racionalnog izraza ne može prijeći stupanj nazivnika
Kako pronaći domenu ograničenja u jednadžbi?
Kako: Za funkciju napisanu u obliku jednadžbe koja uključuje razlomak, pronađite domenu. Identificirajte ulazne vrijednosti. Identificirajte sva ograničenja za unos. Ako u formuli funkcije postoji nazivnik, postavite nazivnik jednak nuli i riješite za x